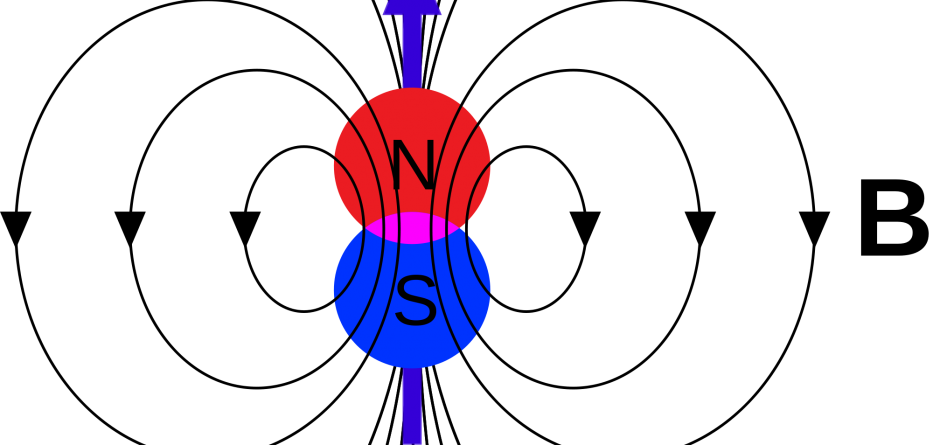
Tanımlar ve Birimler
Birkaç tanım ile başlayalım. Üç tane manyetik vektör vardır. Bunlar;
- H Manyetik Alan
- M Manyetizasyon (Mıknatıslılık)
- B Manyetik İndüksiyon
Birimler üzerine literatürde bir kaç karışıklık vardır. Günümüzde CGS birim sistemi yerine daha çok SI birim sistemi tercih edilir. Manyeto-statiği sunmanın iki yöntemi olduğu için bu karışıklık ortaya çıkar :
- Hayali Manyetik Kutuplar (CGS: santimetre, gram, saniye)
- Akım Kaynakları (SI: Uluslararası Sistem)
Sonuç olarak, temel denklemlerin çoğunun şekli iki sistem arasında farklılık gösterir. Tüm bunlar , bazı keyfi sabitlerin bir sistemde birimleri olduğunu ve diğer bir sistemde ise bire eşit olduğunu gösterir.
Akım ve kutup yaklaşımı arasındaki farklılık birimler konusunda önemlidir. Eski (1980 öncesi) paleomanyetic (ilkel mıknatıslanma) ve kaya manyetiği literatürü esasen CGS biriminde ifade ediliyordu. 4π faktörü de birimlerin önünde yer alır .
Günümüzde SI birim sistemi tercih edildiği için, akım döngüleri ile başlayalım. Elektronların yörüngesinde olduğu bir atoma yaklaşık olarak eşdeğer, r yarıçaplı ve I akımına sahip bir halka düşünelim.
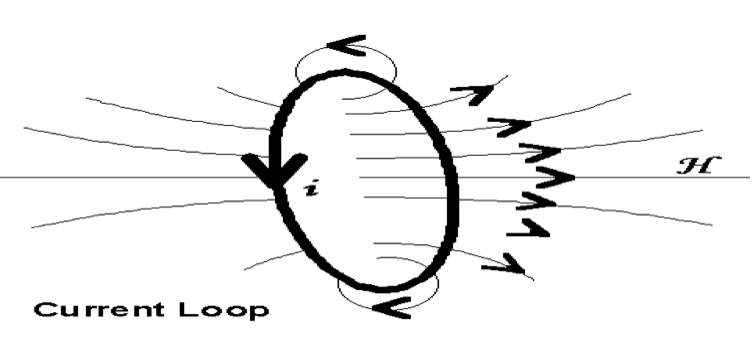
Halkanın merkezinde üretilen H manyetik alan,
H=I/2r [Amper/metre, A/m]
ile verilir.
Bu akım halkasına ayrıca bir manyetik moment (m) eşlik eder :
m=akım x alan=IxA [A.m^2]
Manyetizasyon yoğunluğu (mıknatıslanma yoğunluğu) M veya J, birim hacimdeki manyetik momenttir. M manyetizasyon yoğunluğu olmak üzere
M=m/V [A/m]
ile verilir. M ve H’ nin aynı birimlere sahip olduğuna dikkat edelim.
Birim kütle başına manyetik moment, σ,
σ=m/kütle [(Am^2)/kg]
ile verilir.
Bir diğer temel nicelik manyetizasyonun manyetik alana oranıdır. Bu orana “duygunluk(duyarlılık)” denir.
κ=M/H [Boyutsuz]
Kütle duygunluğu
χ=σ/H=κ/yoğunluk [m^3/kg]
ile verilir.
Duygunluk, bir maddenin bir manyetik alanın varlığında mıknatıslana bilirliğinin bir ölçümüdür ve çeşitli manyetik malzeme sınıflarını tanımlamak için kullanılan genel bir yöntemdir. Bunun ile ilişkili başka bir nicelik ise μ ile gösterilen geçirgenliktir.
SI birim sisteminde B,H ve M arasındaki ilişki
B=μ_0 (H+M) [Tesla,T]
ile verilir. B’ nin birimi Tesla’ dır ve toplam B alanı ortamın manyetizasyonu M ve H alanının toplamına eşittir. Denklemdeki μ_o sabiti serbest uzayın geçirgenliğidir. SI birim sisteminde 4π x 10^(-7) [Henry/m]’ ye eşittir.
Ancak CGS birim sisteminde B,H ve M sayısal olarak bir birine eşit olduğu için μ_0 bire eşittir, ancak, her biri farklı isimlerde birimlere sahiptir (Gauss, Oersted ve emu/cm^3 birimleri, bilim insanlarının ölümünden sonra keyfi olarak seçilmiş ve adlandırılmıştır). CGS birim siteminde
B=H+4πM
ile verilir.
Burada biraz karışıklık oluşur, çünkü CGS birim sisteminde B ve H değiştirilerek kullanılabilir, ancak SI birim sistemine dönüştürüldüğünde farklı sayısal değerleri verir. Örneğin, dünyanın alanı 0.5 Gauss ve ya 0.5 Oe. Ancak, SI birim sisteminde
0.5 Gauss=50 μT [B alanı]
0.5 Oersted=39.8 A/m [H alanı]
Bu örnekte gördüğünüz gibi, Gauss’ u Tesla’ ya dönüştürmek Oersted’ i A/m’ ye dönüştürmekten çok daha kolaydır. Bu yüzden, bütün alanları (B ve H), Tesla’ da belirtmek için paleomanyetikçiler tarafından güncel uygulamada kullanılması çok da şaşırtıcı değildir. B alanının H alanından daha temel bir alan olduğunabir anda karar vermedik(hiçbiri diğerinden daha temel değildir). Aslında, değişen bir alan hakkında konuştuğumuzda ya da 100 miliTesla(mT)’ lık bir manyetik alan dediğimizde, biz gerçekten μ_o H=100mT anlıyoruz. Ancak, bu nadiren dikkate alınır.
Birimler hakkındaki açıklamaları Tablo’ da ki gibi özetleyebiliriz.
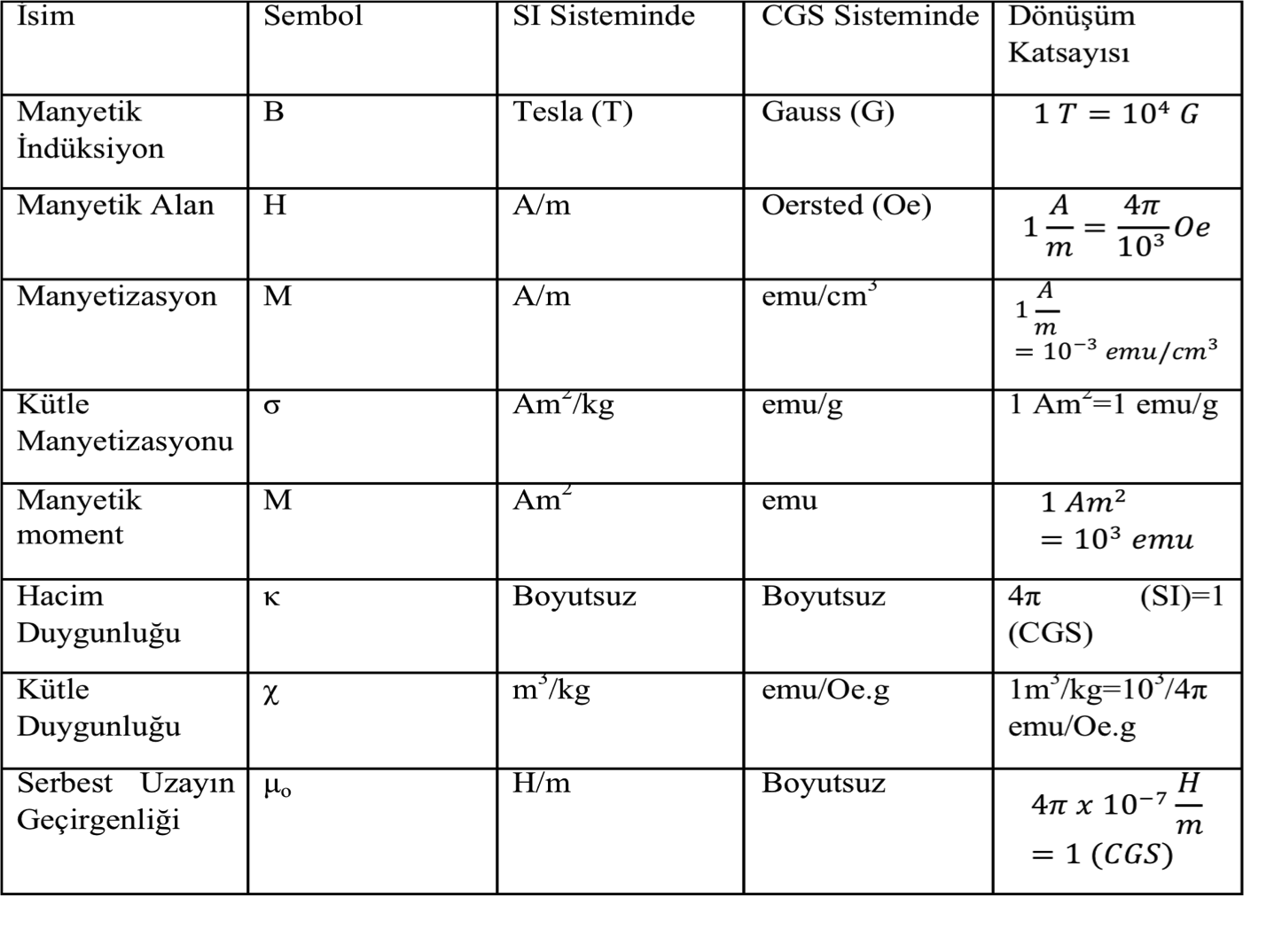
A = Amper
cm = Santimetre
emu = Elektromanyetik birim
g = Gram
kg = Kilogram
m = Metre
H = Henry
Kaynak:
http://www.irm.umn.edu/hg2m/hg2m_a/hg2m_a.html
Sonraki Yazı : Manyetik Malzemelerin Sınıflandırılması