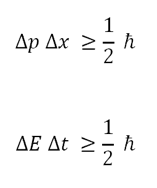SADE GÖZDEN IRAĞIZ BİZ, AYRILSAK DA BERABERİZ

Makroskobik boyutlarda çoğu olay birbirinden bağımsız gibi görünse de, mikroskobik boyutlarda her şey birbiriyle etkileşim halindedir. Sonuçta canlı cansız her şeyin varlığı tek bir kaynağa bağlıdır: Big Bang.

Fakat özellikle bazı maddeler arasında farklı bir iletişim söz konusudur. Bu maddelerin birbirine çok yakın olması veya birbirlerinden ışık yılı hatta daha fazla uzaklıkta bulunmaları fark etmeksizin, birisinde meydana gelen değişiklik eş zamanlı olarak, diğerinde de etkiye neden olur. Buna kuantum dolanıklık denir.

Bir sonuç olan kuantum dolanıklık yerine, önce bu dolanıklığa sebep olan, sistemin alt birimleri arasındaki etkileşimi sorgulayalım.

Bu etkileşimi incelemeye, kuantum mekaniğinden önce fizik tarihinde dönüm noktalarından biri olan ve kendinden sonraki birçok gelişimin temelini oluşturan klasik fizikten başlayalım.

Klasik fiziğin kurucusu Isaac Newton, bir sistem parçalandığında, her bir parçanın, korunum yasalarınca, kesin ve iyi tanımlanmış bir enerjisi, momentumu ve açısal momentumu olduğunu savunur. Yani her bir alt sistemin özellikleri tamamen bağımsızdır. Yaşadığımız dünyada, makroskobik boyutlarda, bu tezin geçerli olmasının sebebi, Newtonian sistemin yerel/local olmasıdır.

Peki ya yerel olmayan/nonlocal bir kuantum sistemi parçalarsak neler olur?

Kuantum sisteminin “nonlocal” özelliği ilk kez Einstein ve arkadaşları Podolsky ve Rosen tarafından 15 Mayıs 1935’te Physical Review dergisinde yayınlanan EPR Bildirisi’nde gündeme gelmiş olsa da meselenin kaynağı, 1927’lerde Heisenberg’in çalışmalarında kullandığı “tamamlayacılık felsefesi”ne dayanır.

Çevremizde gördüğümüz kilit-anahtar, ampul-elektrik ve anne-çocuk örneklerinde, biri olmadan diğerinin de olamayacağını veya olsa bile beraber olduklarındaki işlevi yerine getiremeyeceğini hepimiz biliriz. Buna “tamamlayıcılık felsefesi” denir.

Bizim günlük hayatta kurduğumuz bu ilişkiyi, Heisenberg, fizikte konum-momentum ile enerji-zaman arasında kurdu ve bunları “tamamlayıcı değişkenler” olarak adlandırdı.

Heisenberg yaptığı deneysel gözlemlerden, bir değişkenin değeri artarken, diğerinin değerinin azaldığı ve değişken değerlerinin çarpımının bir sabite eşit olduğu sonucuna vardı.
Bunu kuantum mekaniğe uyarlayarak,1927’de yayınladığı Belirsizlik İlkesi’ni türetti. Bu ilkeye göre, bir parçacığın, aynı anda konumu ve momentumu kesin bir şekilde bilinemez, diğer bir deyişle, birinin değeri ne kadar kesin bir şekilde tespit edilirse, onun tamamlayıcısı olan diğerinin değeri o ölçüde belirsiz olarak saptanacaktır.

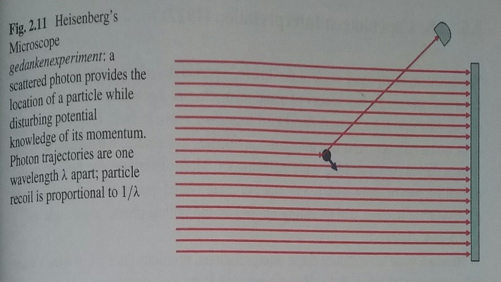
Heisenberg, Belirsizlik İlkesi’ni daha detaylı açıklayabilmek için, sonrasında “Heisenberg’in mikroskobu” olarak da adlandırılan, bir düşünce deneyi (gedankenexperiment) geliştirdi.
Deneyde, boş uzayda herhangi bir yerde lokalize olan bir parçacık düşündü ve konumunu ölçmek istedi. Bu amacını, parçacığı, çeşitli konum olasılıklarından geçen bir dizi fotonla vurarak gerçekleştirdi. Çünkü fotonlardan birinin ilgi parçacığı tarafından Compton Saçılımı yaptığı gözlemlendiğinde, parçacığın bu fotona karşılık gelen konumda olduğu bilinir. Bu deney, çocukken oynadığımız misket vurma oyununa benzer. Bir misketi vurmak için farklı konumlardan birçok misket gönderilse de,1. misketi vurmanın en iyi yolu, mümkün olduğunca o misketin hizasında ve ona en yakın pozisyonda, 2. Misketi 1. miskete vurmaktır.

Böyle bir ölçümde konum hassasiyeti, fotonun dalga boyu ile kısıtlanmış olur. Yüksek frekanslı radyo dalgaları gönderildiğinde, parçacık birkaç cm hassasiyetle bulunurken, gama ışınları gönderildiğinde birkaç yüz fm hassasiyetle saptanır. Yani gönderilen fotonun dalga boyu azaltıldıkça, parçacığın momentumu daha kesin bir şekilde tespit edilir. Tabii ki parçacığın yaptığı her bir Compton Saçılımı, onun üzerinde farklı bir etkiye sahip olduğundan ve parçacığın ilk momentum değeri ile yaptığı compton saçılmasının detayları bilinmediğinden, parçacık belirsiz olan yeni bir momentum değerine sahip olur.

Bu durum “Bozulma Modeli” olarak adlandırıldı ve ilk kez Bohr tarafından yanlışlığı gösterildi.

Çünkü burada, parçacığın konumunun ve momentumunun, klasik fizikte olduğu gibi, aynı anda iyi bir şekilde tanımlanabileceği fakat kaba ölçüm yöntemlerinin sınırlamaları nedeniyle her ikisinin aynı anda doğru ölçülemediği varsayılıyor.

Halbuki bu varsayım, Heisenberg’in keşfettiği dalga mekaniği formalizminin mesajı değildir.

Gerçek mesaj, parçacığın eş zamanlı iyi tanımlanmış konum ve momentumu olamayacağını ve bu özelliğin parçacığın temel bir özelliği olduğunu, yani üzerinde gerçekleştirilen ölçüm seçiminin veya kalitesinin hiçbir ilgisi olmadığını ifade eder. Yapılan ölçümler sadece, bir değişkenin bazı keyfi hassasiyet gösterebildiği değerler aralığını kısıtlayabilir.

Bu tamamlayıcılık felsefesinden yola çıkılarak türetilen Belirsizlik İlkesi,1927’den sonrasına yeni bir kuantum mekaniği teorisi teslim etti, tabii ki bazı yorumlama sorunlarıyla beraber…

Bir benzetme ile açıklayacak olursak; fizik gelişimini kapalı bir odaya, klasik mekaniği de bu odanın tabanı olarak varsayımda bulunursak, kuantum mekaniği, odanın içine atılan ve duvarları yıkacak potansiyele sahip bir bombanın fitili şeklinde düşünebiliriz. Bu bombayı atan kişiler başta Werner Heisenberg, Erwin Schrödinger, Niels Bohr, Max Born, Albert Einstein, liderliğinde pek çok kuantum mekaniği savunucusudur.
“Kopenhag Yorumu” ve “EPR Bildirisi” ise bu fitili çekerek fizik gelişiminin, tek bir odadan koca bir evrene yayılmasını sağlayan yani sonu olmayan yeni bir ufuk kazandıran iki önemli gelişmedir. Patlayan bombanın etkisiyle etrafa yayılan inşaat malzemeleri ve toz ise kuantum fiziğinin yorumsal sorunlarını simgeler. Kopenhag yorumu, Belirsizlik İlkesi’nden sonra, Bohr, Heisenberg ve Born tarafından,1927’de Brüksel’de düzenlenen 5. Uluslararası Solvay Konferansı’nda sosyeteye tanıtılan ve akabinde kuantum mekaniği formalizminin standart yolu haline gelen bir yorumdur.

Niels Bohr

Werner Heisenberg

Max Born

Bu yorumun ana ilkeleri şöyle özetlenebilir:

1)Bir sistem tamamen, bir dalga denklemi karakteristiğinin çözümü olan bir dalga fonksiyonu tarafından tanımlanır. Bu dalga fonksiyonu, sistem gözlemcisinin matematiksel bir temsilidir ve bilgi değiştiğinde değişir.

2)Bir sistemin gözlemlenebilir niceliklerine odaklanılmalı ve ölçüme tabi olmayan yönler hakkında soru sormaktan kaçınılmalıdır.

3)Doğanın kuantum mekanik tanımı, olasılıklı ve rastlantısaldır. Özdeş koşullar farklı sonuçlar doğurabilir.

4)Bir sistemin aynı anda tüm özelliklerinin kesin değerlerini bilmek mümkün değildir, tamamlayıcı değişkenler Belirsizlik İlkesi’ne tabidir, bilinmeyen özellikler olasılıklarla tanımlanır.

5)Madde ve ışık, dalga-parçacık ikiliğini gösterir; bir deney parçacık-benzeri ya da dalga-benzeri özellikleri gösterebilir, ancak ikisini de aynı anda gösteremez. Belirsizlik İlkesi, dalga-parçacık çatışmalarını önler.

6)Büyük kuantum sayılarının limiti içindeki bir sistemin kuantum mekanik tanımı, onun klasik tarifine çok yakın bir şekilde karşılık gelmelidir. Yani kuantum sayılarının büyüklüğü arttıkça, sistem, kuantum mekaniğinden klasik mekaniğe doğru kayar.

Fakat Einstein, bu yorumu sevmedi ve onun kabul edilmemesi için 1930’da Brüksel’de manyetizma üzerine düzenlenen 6. Uluslararası Solvay Konferansı’nda Belirsizlik İlkesi’ni ihlal ettiği gerekçesiyle saat paradoksunu sunsa da, Bohr tarafından bu paradoksun yanlışlığı gösterildi ve bilim camiası Bohr’un başarısını kabul etti.

Einstein’ın Kopenhag Yorumu’na karşı çıkmasının sebebi, kendisine göre kuantum mekaniğinin yalnızca olasılık ile yorumlanıp, üstünün kapatılmasının yanlış olması ve kuantum mekaniği özelliklerinin daha iyi incelenmesinin gerekliliğidir.

Nitekim Einstein, Max Born’a yazdığı bir mektupta: ”Hiçbir zaman, hiçbir koşulda, beni Tanrının zar attığına ikna edemezsiniz.” demiştir.

Einstein da Bohr da, bir parçacığın uzay-zamanda konumu ile momentumunun aynı anda bilinemeyeceği, yalnızca istatistiksel olarak orbitaller aracılığıyla tahmin edilebileceği konusunda hemfikirdir. Fakat, Bohr, indeterminizm yolunu seçerek bu durumun fiziğin tamamlayıcılık ilkesi ile tutarlı olduğunu savunmuş, Einstein ise determinizm yolunu seçerek, bu istatistiksel sistemin tümüyle rastgele olmuş olamayacağını, arkasında mutlaka bir model, bir plan var olması gerektiğini iddia etmiştir.
Bunun üzerine, yılmayan Einstein,1935’te arkadaşları Boris Podolsky ve Nathan Rosen ile birlikte yayınladıkları, soy isimlerinin baş harflerinden oluşan EPR Bildirisi’nde, kuantum mekaniğinde fark edilmemiş 2 kusuru sundu.

Albert Einstein

Boris Podolsky

Nathan Rosen

Bombanın fitilini çeken diğer bir el olan EPR Bildirisi’nin 1. bölümünde, kuantum sistem tanımındaki Belirsizlik İlkesi’nin dalga-parçacık ikiliğindeki rolü üzerine itiraz edildi.

Buna göre, eğer konjuge fiziksel niceliklerden bir çiftin bir üyesinin bilgisi, diğer üyenin bilgisini engelliyorsa;

(i)ya kuantum mekaniğinde dalga fonksiyonu tarafından verilen gerçekliğin açıklaması tam değildir.

(ii)ya da iki konjuge nicelik eş zamanlı gerçekliğe sahip olamaz.

Yani, bir sistemin dalga-benzeri davranışıyla, parçacık-benzeri davranışı birbiriyle çatışıyorsa;

(i)ya bu sistemi tanımlayan dalga fonksiyonunun gerçeklik açıklamasında eksik bir şeyler vardır.

(ii)ya da bu sistem, dalga-benzeri ve parçacık-benzeri davranışlara aynı anda sahip olamaz.

bölümünde ise, daha önce fiziksel temas halindeyken, ayrılmış 2 sistemin durumu hakkında kuantum tahminler yapma meselesi üzerinde duruldu ve momentum korunumu, kuantum mekaniğinin nonlocal olarak göründüğünü iddia etmek için kullanıldı.

Önce; bir sistemde hangi niceliğin(konum veya momentum) ölçüleceğini seçmenin, diğer sistem üzerinde yapılan olası ölçüm sonuçlarını etkilediği tartışıldı.

Sonra; sistemler artık etkileşime girmediğinden, ilk sisteme yapılabilecek herhangi bir şeyin sonucunda,2. Sistemde hiçbir gerçek değişim olamayacağı tartışıldı.

Bildirinin 2. bölümünde ortaya çıkan konular “EPR Paradoksu” olarak bilinir.

Bu görünen çelişki,(ii) olasılığının olamayacağını iddia etmelerine yol açtı ve bu nedenle kuantum mekaniğinin eksik olması gerektiğine inanıldı.

Peki, kuantum mekaniğinde ne eksikti?

Eksik olan şey, mekansal olarak ayrılmış sistemler üzerinde gerçekleştirilen ölçümler arasındaki korelasyonların uygulamaları ve kuantum mekanik formalizmin nonlokalitesi idi.

Einstein, nonlokaliteye “bir mesafedeki ürkütücü eylemler” (“spooky actions at a distance”) olarak atıfta bulunmuştur.

Erwin Scrödinger

Schrödinger, EPR Paradoksunu ciddiye alıp, araştırdı ve çok parçalı bir kuantum sistemin bileşenlerinin birbirlerinden ne kadar uzak olurlarsa olsun nasıl bağlı kala

cağını detaylı bir şekilde gösterdi. Buradan yola çıkarak, dalga fonksiyonları mekansal olarak ayrı ve ışık hızlı temastan uzak olan sistem parçalarını tanımlasalar dahi, ayrılmış dalga fonksiyonlarının birbirine bağlı olmaya devam ettikleri ve ayrı olarak tanımlanamayacakları anlamına gelen “dolanıklık”(“entanglement”) terimini gündeme getirdi. Ancak nonlokalitenin geçerliliği hakkında yine de şüphe duyduğunu belirtti.

David Bohm

1951’de EPR destekçisi David Bohm, paradoksal özelliklerin ihlal edildiği, EPR Bildirisi’nin itiraz ettiği standart kuantum mekaniği ile yer değiştirebilecek ve tüm korelasyonların yerel/local olarak düşük hızlarda oluşturulduğu bir “Yerel Gizli-Değişken Teorisi”(“local hidden-variable theory”) ortaya attı. Fakat EPR deneyleri, yerellik ile ilgili sorunları göstererek bu “yerel gizli-değişken teorisi”ndeki,”gizli-değişkenler”inde değil, fakat ”yerellik(lokalite)” durumunda ters giden bir şeyler olduğunu gösterdi.

John Stewart Bell

1964’te test edilebilirlik durumu değişti.

İrlandalı fizikçi John Stewart Bell, deneysel testlerin kuantum mekaniği tahminlerini herhangi bir yerel gizli-değişken teorisinden nasıl ayırt edilebildiğini gösteren şaşırtıcı bir teoriyi kanıtladı.

Bell, hesaplamalarını, Einstein ve Scrödinger’in argümanlarının ilgi odağı olan konum ve momentum ölçümlerine değil, açısal momentum korunumunun göz önüne alındığı ışık fotonlarının lineer polarizasyon ölçümlerine dayandırdı.

Bell’in teoreminden önce, ona ilham veren ışığın polarizasyonunu ele alalım.

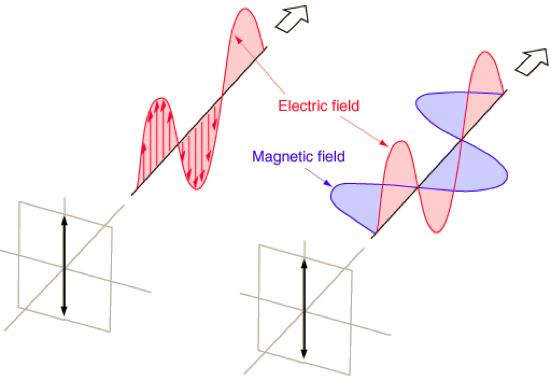
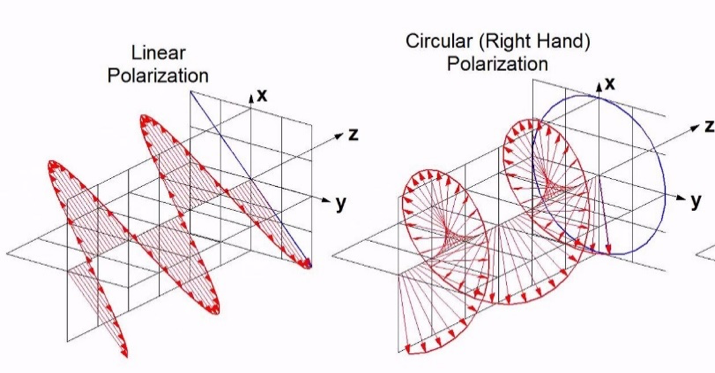
Işık olarak gördüğümüz olaylar(görünür, görünmez ışık, ultraviyole ışınlar, gama ışınları, X-ışınları…),ışık hızında uzayda hareket ederken, elektrik ve manyetik alanlar birbirine dik açılarla birlikte titreştiğinde üretilen hareketli dalgalardır. Bir ışık dalgasının elektrik yönü, dalganın polarizasyonunu belirler.

Elektrik alanı daima aynı düzlemde titreşirse, bunun polarizasyon düzlemi olduğunu ve dalganın bu düzlemde lineer polarizasyonu olduğunu; ışık dalgası ilerledikçe, elektrik alanı uzaya doğru sağa ve sola sarmal olarak kıvrılırsa, dalganın dairesel polarizasyonu olduğunu söyleriz.

Lineer polarizasyon, sol ve sağ dairesel polarizasyonun uygun faza sahip durumlarının üst üste bindirilmesiyle oluşurken; dairesel polarizasyon, dikey ve yatay lineer polarizasyonun üst üste bindirilmesiyle oluşur.

Bell teoremi ile yapılan çalışmaların çoğu, lineer polarizasyon durumlarına odaklanmıştır.

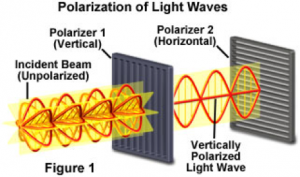
Bir ışık demetini iki demete bölen polarizasyon-duyarlı dağıtıcılar kullanılarak, gelen ışığın belirli bir polarizasyon bileşeni iletilebilir ve diğer bileşen emilir veya dağıtılabilir.

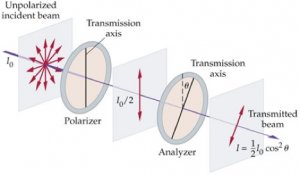
Polarize olmamış bir ışık demeti, önce böyle bir polarizasyon filtresinden geçirildikten sonra diğerinden geçirilirse, iletilen ışığın yoğunluğu Malus Yasası’na göre değişir.

Malus Yasası’na göre, iletilen ışının yoğunluğu I ( θ ) ,1. filtrenin polarizasyon yönü ile 2. filtrenin polarizasyon yönü arasındaki açının θ cosinüsünün karesi ile orantılıdır.

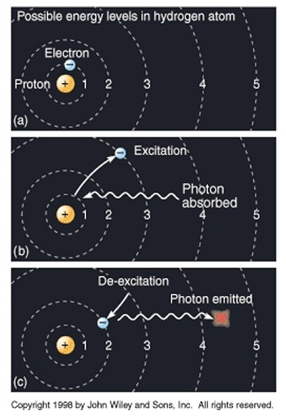
Bir atomda eğer bir yörünge elektronu, en düşük enerji seviyesinden, enerjik bir foton ya da elektriksel boşalma ile daha yüksek bir yörüngeye atılırsa; elektron,”kaskad”(“cascade”) olarak adlandırılan bir işlemle en düşük enerji durumuna geri dönebilir.
Yani, daha düşük yörüngelere, her bir sıçramanın kendi enerji boşluğuna bağlı olan bir dalga boyundaki tek bir ışık fotonu üreten bir dizi ”kuantum sıçrama” (quantum jumps”) olur.

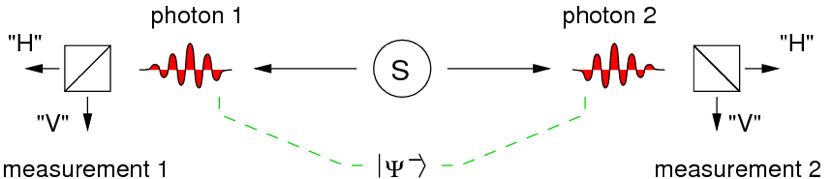
Atomun bir bütün olarak,net açısal momentum olmadan (yani dönme hareketi olmadan) başlayıp bittiği ve “parite”nin değişmediği (yani sistemin ayna-simetrisinin değişmediği) 2 fotonlu bir kaskad özellikle dikkat çekicidir, çünkü kaskad, açısal momentum korunumundan dolayı polarizasyonlarla ilişkili olan dolanık bir foton çifti üretir.

Diğer bir deyişle, kaskadtan gelen fotonlar, zıt yönlerde, arka arkaya hareket ettiğinde; fotonlardan birinin belirli bir lineer polarizasyon durumuna sahip olduğu ölçülürse, açısal momentum korunumu, diğer fotonun da tam olarak aynı lineer polarizasyon durumuna sahip olmasını gerektirir.

Genellikle “EPR Deneyleri” olarak adlandırılan, 1970’lerdeki Bell teoreminin ilk deneysel testi, bu gibi kaskadlardaki dolanık foton çiftlerini kullandı.

Bu EPR deneyleri, her foton, polarize edici bir filtreden geçtikten sonra kuantum-duyarlı fotoçoğaltıcı tüpler tarafından tespit edildiği şekilde, cihazın karşı uçlarındaki dolanık fotonların rastlantısal varışını ölçtü.

Cihazın zıt uçlarındaki fotoçoğaltıcılar, aynı anda ortaya çıktıklarında bir “rastlantı” veya iki foton olayı olarak kaydedilen elektrik palsları üretirler.

Bu tür rastlantısal olayların oranı iki filtrenin polarizasyon “geçiş” yönlerini değiştirirken iletim-ekseni açıları α₁ve α₂ile karakterize edilerek ölçülür. Ölçüm, tam bir grafik geliştirilene kadar tekrarlanır.

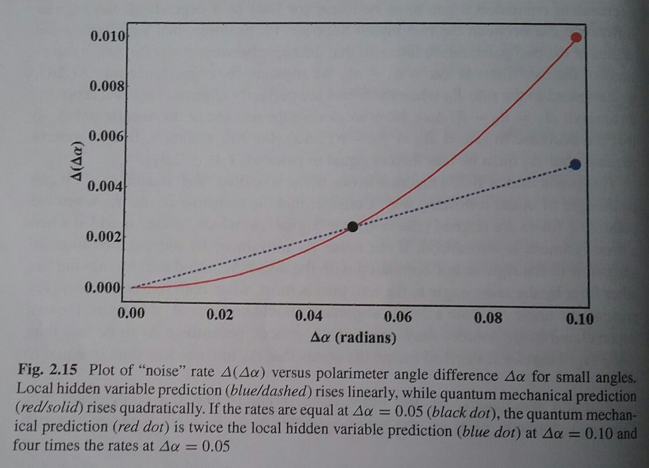
Bell teoremi, iki iletim açısının α₁ ve α₂ eşit olmadığında, bir EPR deneyinin rastlantısal oranının düşme biçimiyle ilgilenir.

Sonuç olarak Bell, tüm yerel gizli-değişken teorileri için, rastlantısal orandaki azalmanın büyüklüğünün lineer (veya daha az) olması gerektiğini matematiksel olarak gösterdi. Bu sonuç,”bell eşitsizlikleri” denilen şeylerden biridir.

Diğer taraftan kuantum mekaniği, Malus Yasasınca, rastlantısal oranın, karesel olarak düşmesi gerektiğini öngörür-ki bu da açıkça Bell eşitsizliğinde belirtilenden daha büyüktür.

Bu, Bell teoreminin açık bir ihlalidir. Çünkü kuantum mekaniği tarafından tahmin edilen rastlantısal oran artan açıyla çok hızlı bir şekilde düşerken, Bell teoremi lineer bir azalmayı öngörür.

Bu durumda, kuantum mekaniği ve yerel gizli-değişken teorileri arasındaki fark nedir?

Lineer ve kuadratik davranış arasındaki temel fark Bell eşitsizliklerinin kökenindedir.

Çünkü Bell, gerçek tek foton dedektörlerinin %100 ünden daha az verimini ve gerçek polarizasyon analizörlerinin mükemmel olmayan davranışını göz önüne almadı.

Bunun üzerine, John Clauser’ın liderlik ettiği bir grup, Bell eşitsizliğinin daha gerçekçi bir deneysel bağlamda toplanmasının zorunlu olduğu CHSH eşitsizliğini üreterek, yukarıda söylenen etkileri hesaba katmak için bell teoremini genelleştirdi.

Stuart Freedman

John F. Clauser

1972’de Stuart Freedman ve John F. Clauser’ın öncü deneysel çalışmasından başlayarak, Bell eşitsizliğini ihlal eden ve dolanık

kuantum sistemlerinin diğer yönlerini test eden bir dizi kuantum optik EPR deneyleri gerçekleştiridi.

Bu EPR deneysel örneklerinden birisi,1998’de İsviçre’deki Gisin Grubu tarafından gösterildi.

Gisin Grubu, İsviçre Telefon Sistemi’ne ait fiber optik kabloları, Cenevre’de, Bern’de ve İsviçre’de 156 km lik bir görüş hattı ayrılığıyla yapılan EPR ölçümleri arasındaki nonlocal bağlantıyı göstermek için kullandılar.

Bu çalışmada, sadece kuantum mekaniği nonlokalitesinin varlığına değil, aynı zamanda bu tür nonlokalitenin oldukça geniş uzamsal ayrımlar üzerinde gerçekleştirilebileceğine bir delil oluşturdu.

Böylece EPR deneyleri, yerel gizli-değişken teorilerine dayanan Bell teoremindeki “yerelliği” sorgulayarak, kuantum mekaniği nonlokalitesi için doğrudan bir ispat olarak gösterildi.

Şu da belirtilmelidir ki, polarizasyona dayalı EPR deneyleri, doğanın ayrılmış sistemlerinin üzerinde gerçekleştirilen ölçümlerin korelasyonlarını düzenlemek için bazı nonlokal mekanizma kullandığının gösterimi olarak alınabilirken, böyle bir ışık hızından daha hızlı telgraf hattı, deneyciler tarafından kendi mesajlarını göndermek için erişilebilir değildir.

Yani, yukarıda bahsettiğimiz dolanık foton çifti örneğinde, her gözlemci, ölçüm için polarizasyon temeli seçme konusunda özgürken, fotonu, nonlokal iletişimde gerekli olduğu gibi, bu temelde belirli bir duruma zorlamakta özgür değildir.

Kısacası, Einstein’ın “bir mesafedeki ürkütücü eylemler” olarak gördüğü “nonlokalite”,doğanın kuantum düzeyinde işleyiş biçiminin önemli bir parçasıdır.

REFERANSLAR:

Bigaj, T. F. (2006). Non-locality and possible worlds : a counterfactual perspective on quantum entanglement. Frankfurt ; New Brunswick, N.J. : Ontos ; Piscataway, N.J. : North and South America by Transaction Books, Rutgers University, 2006.
The quantum handshake. (2015). New York, NY : Springer Berlin Heidelberg, 2015.

Ana Görsel Kaynak: https://tomajjavidtash.com/tag/quantum-entanglement/

RESİMLER İÇİN KAYNAKÇA

Çocuk misketi: http://www.tipeez.com/ch/hurriyet/news/eda/3934/sokak-oyunu.aspx

Polarizer: http://slideplayer.com/slide/10590490/

Malus law: http://www.memrise.com/mem/1092901/malus-law/

Uncertainty principle: http://hendrix2.uoregon.edu/~imamura/122/lecture-6/hup.html

Max born: https://en.wikipedia.org/wiki/Max_Born

Bohr: https://www.tamseo.com.tr/niels-bohr/

Heisenberg: http://www.kwanty.friko.pl/poczet.php

Einstein: https://en.wikipedia.org/wiki/Albert_Einstein

Podolsky: https://www.titanians.org/about-bob-podolsky/

Rosen: http://www.setcelebs.com/nathan-rosen.html